Triángulo de Pascal
El triángulo de Pascal en matemáticas es un conjunto infinito de números enteros ordenados en forma de triángulo que expresan coeficientes binomiales. El interés del Triángulo de Pascal radica en su aplicación en álgebra y permite calcular de forma sencilla números combinatorios lo que sirve para aplicar el binomio de Newton. También es conocido como Triángulo de Tartaglia. En países orientales como China, India o Persia, este triángulo se conocía y fue estudiado por matemáticos como Al-Karaji, cinco siglos antes de que Pascal expusiera sus aplicaciones, o por el astrónomo y poeta persa Omar Jayyam (1048-1123). En China es conocido como Triángulo de Yanghui, en honor al matemático Yang Hui, quien lo describió el año 1303.
Composición del Triángulo de Pascal
El Triángulo se construye de la siguiente manera: escribimos el número «1» centrado en la parte superior; después, escribimos una serie de números «1» en las casillas situadas en sentido diagonal descendente, a ambos lados; sumamos las parejas de cifras situadas horizontalmente (1 + 1), y el resultado (2) lo escribimos debajo de dichas casillas; continuamos el proceso escribiendo en las casillas inferiores la suma de las dos cifras situadas sobre ellas (1 + 2 = 3)...
Las cifras escritas en las filas, tales como: «1 2 1» y «1 3 3 1» recuerdan los coeficientes de las identidades:
Vínculo entre el triángulo de Pascal y el binomio de Newton
La expresión que proporciona las potencias de una suma  se denomina Binomio de Newton.
se denomina Binomio de Newton.
 se denomina Binomio de Newton.
se denomina Binomio de Newton.(1)
En esta expresión, lo único que se desconoce son los coeficientes de los monomios.
Los coeficientes de la forma desarrollada de (a + b)n se encuentran en la línea «n + 1» del Triángulo de Pascal. |
Hemos visto que era cierto para n = 2 y n = 3; también lo es para n = 0: (a + b+ w+ d)o = 1 = 1·aob0 y con n = 1: (a + b)¹ = a + b = 1·a + 1·b.
Para obtener el resultado de cualquier valor de n ∈ N, se procede por inducción matemática. Suponiendo que es cierto para un valor de n, deducimos que lo es también para n+1. Observemos lo que sucede con n = 4.
El desarrollo de (a + b)4 consiste en el desarrollo de (a + b) (a + b)³.
Si sólo se escriben los coeficientes, obtenemos la siguiente suma:
Coeficientes del binomio de Newton
Se inscribe el triángulo de Pascal en una tabla para poder nombrar a cada coeficiente del mismo. El número en la línea n y la columna p se denota:
o más raramente
(C por "combinación") y se dice "n sobre p", "'combinación de n en p"' o "coeficiente binomial n, p". Las casillas vacías corresponden a valores nulos. Por definición misma, tenemos, (para todo n natural):
para cualquier valor de a y b. De hecho, es una igualdad de polinomios en Z[a, b]. Sin perder en generalidad, resulta a veces más práctica la definición:
vista como una igualdad de polinomios en Z[X]. De esta fórmula se deducen dos consecuencias:
| Tomando X = 1 se obtiene: |  |
La suma de los coeficientes de una misma línea vale 2n. En efecto: 1 = 20,1 + 1 = 2 = 21,1 + 2 + 1 = 4 = 22,1 + 3 + 3 + 1 = 8 = 23,1 + 4 + 6 + 4 + 1 = 16 = 24... Con X = − 1 se obtiene, (n > 0):
 | : la suma alterna de los números de una misma línea vale 0. |
En efecto: 1 − 1 = 0,1 − 2 + 1 = 0,1 − 3 + 3 − 1 = 0,1 − 4 + 6 − 4 + 1 = 0,1 − 5 + 10 − 10 + 5 − 1 = 0.... Las propiedades que hemos observado en el triángulo se pueden ahora escribir con todo rigor:
| . |
 | (costados izquierdos y derechos del triángulo). |
| . |
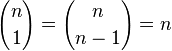 | ("segunda capa"). |
| . |
 | (simetría respecto al eje vertical del triángulo). |
| . |
 | cuando p > n (corresponde a la zona fuera del triángulo). |
Y claro, la regla de construcción del triángulo da la relación fundamental de los coeficientes binomiales:
| . |

por todo lo anterior notamos estas similitudes y la mente de estos grandes genios que fueron Pascal y Newton.




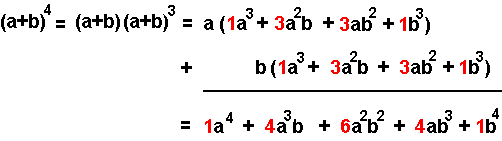

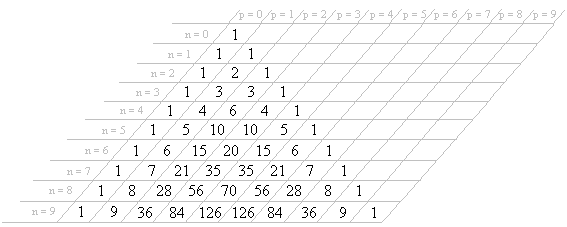


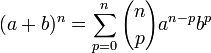
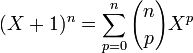

No hay comentarios:
Publicar un comentario